Однозначная интерпретация всех инструкций алгоритма

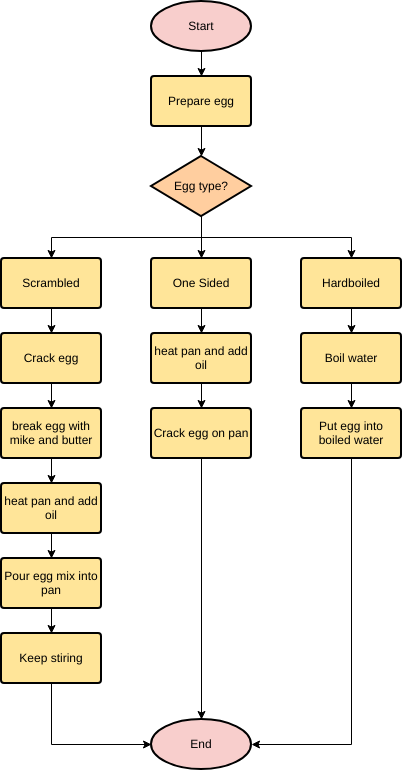
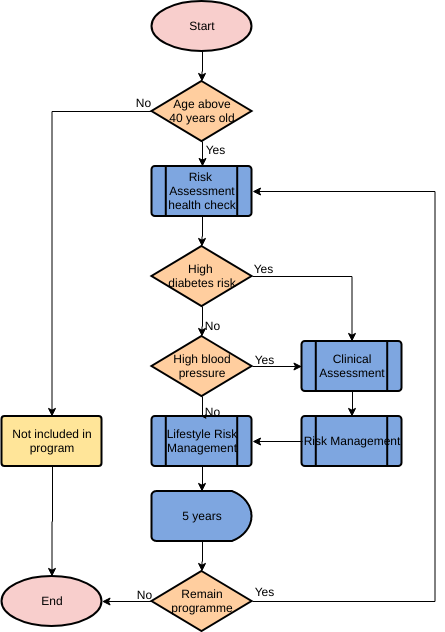
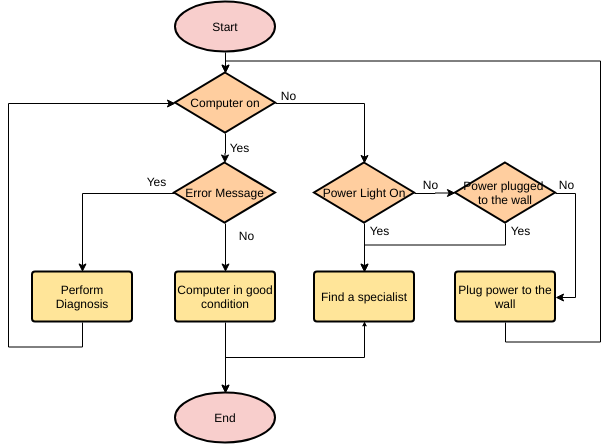
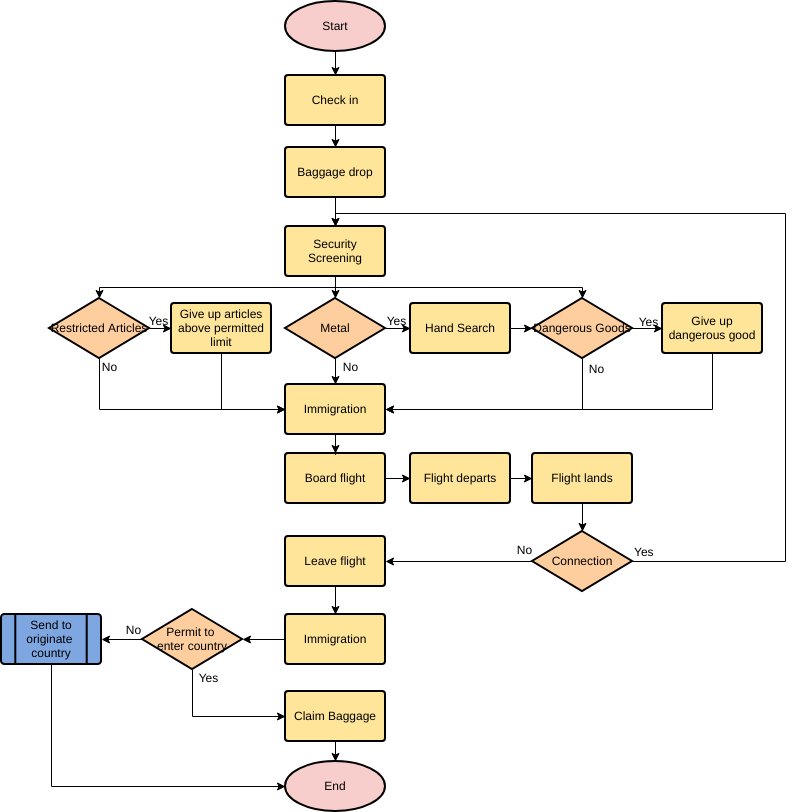
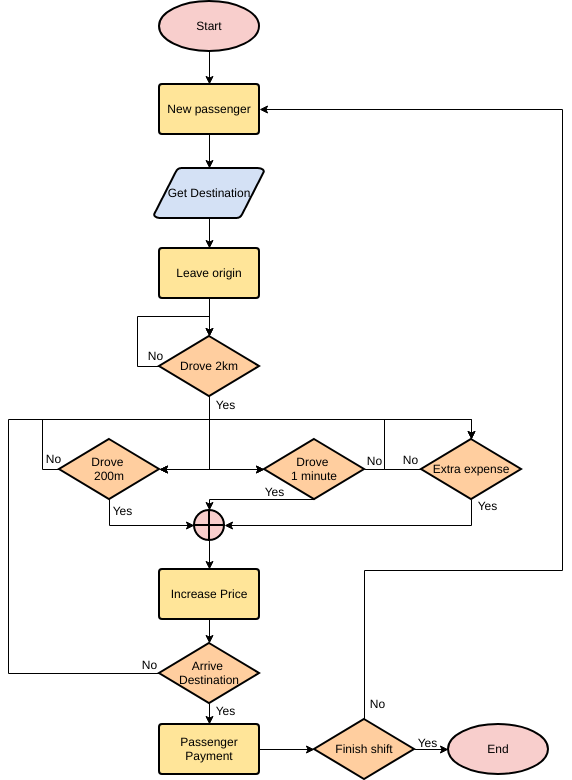
Алгоритм. Свойства алгоритмов.
Блок-схемы. Алгоритмические языки

Код ОГЭ: 1.3.1. Алгоритм, свойства алгоритмов, способы записи алгоритмов.
Блок-схемы. Представление о программировании

Понятие алгоритма является одним из основных понятий вычислительной математики и информатики.

■  Алгоритм
— строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.

Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.

Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.

В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.

Свойства алгоритмов

Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:

• Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
• Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
• Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
• Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
• Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.

Способы представления алгоритмов:

• словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
• блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
• формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
• псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.

Словесная запись алгоритма

Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.

■  Пример 1. Записать в словесной форме правило деления обыкновенных дробей.

Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.

Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).

Формальные исполнители алгоритма

Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.

Программы на языке произвольного формального исполнителя могут состоять только из элементарных команд, которые входят в его систему (которые исполнитель «понимает»).

Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.

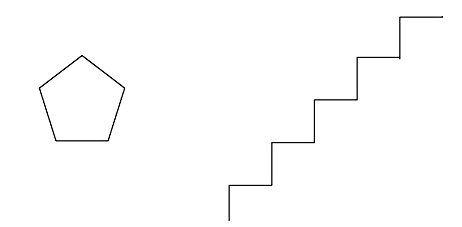
■ Пример 2. Исполнитель Крот имеет следующую систему команд:

1. вперед k — продвижение на указанное число шагов вперед;
2. поворот s — поворот на s градусов по часовой стрелке;
3. повторить m [команда1 … командаN] — повторить m раз серию указанных команд.

Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?

Повторить 5 [вперед 10 поворот 72]

Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.

Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).

■ Пример 3.  В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).

Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).

Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]

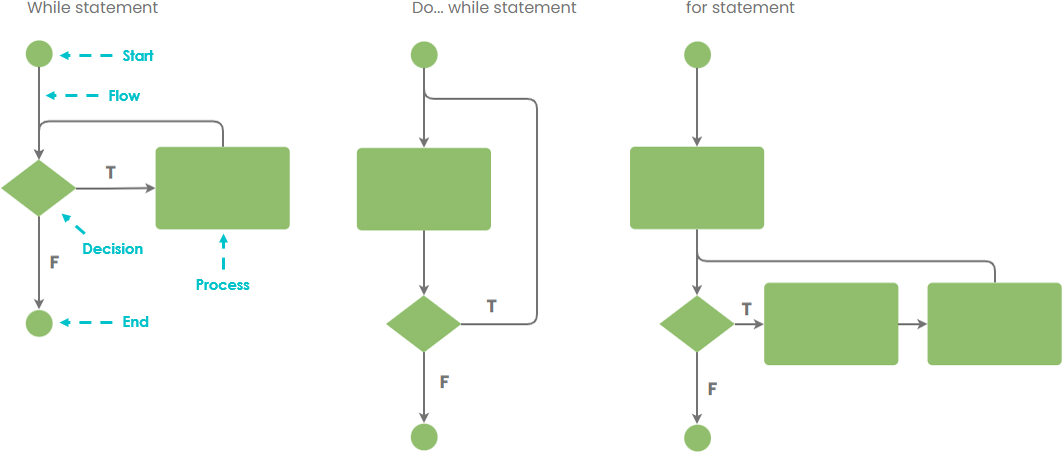
Блок–схема

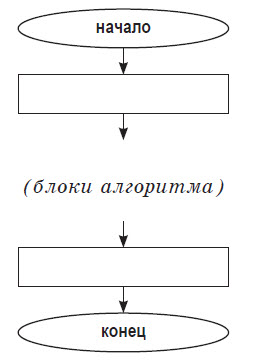
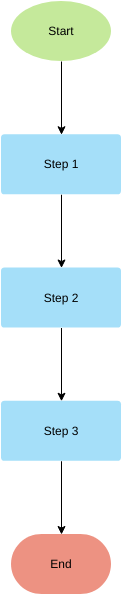
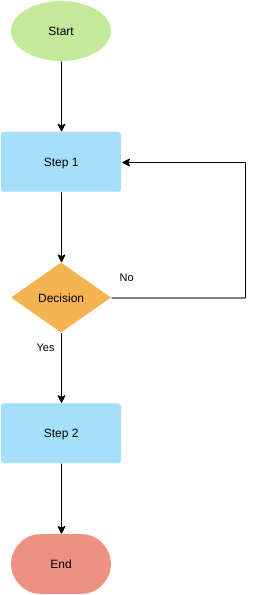
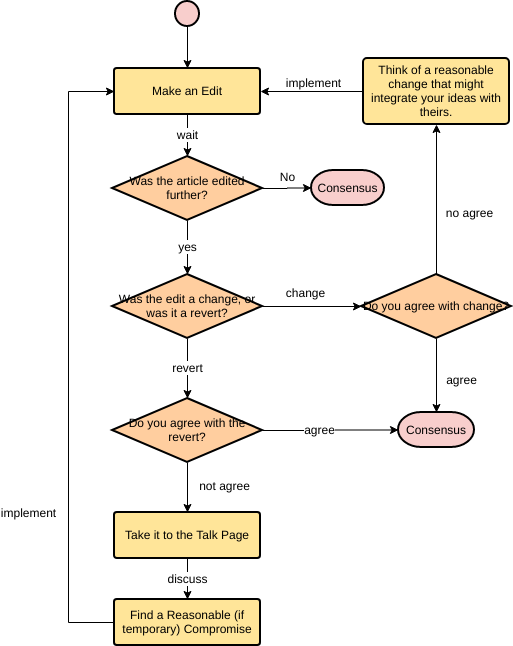
Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).

Основные элементы блок–схемы алгоритма:

Общий вид блок–схемы алгоритма:

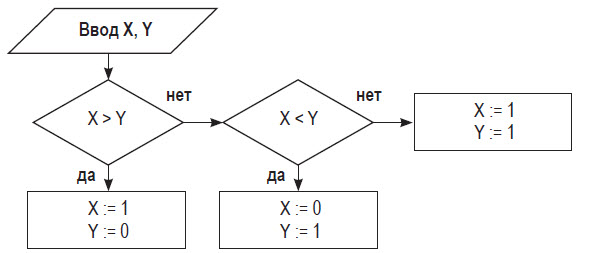
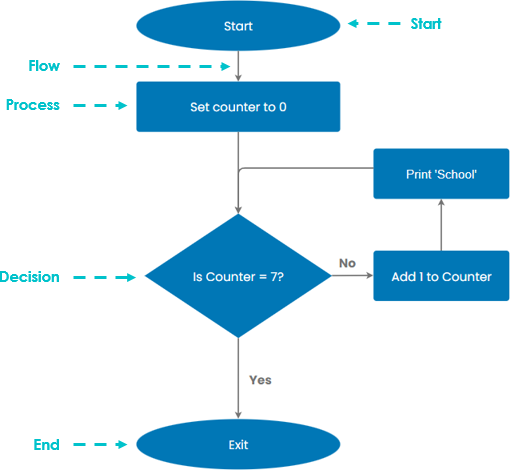
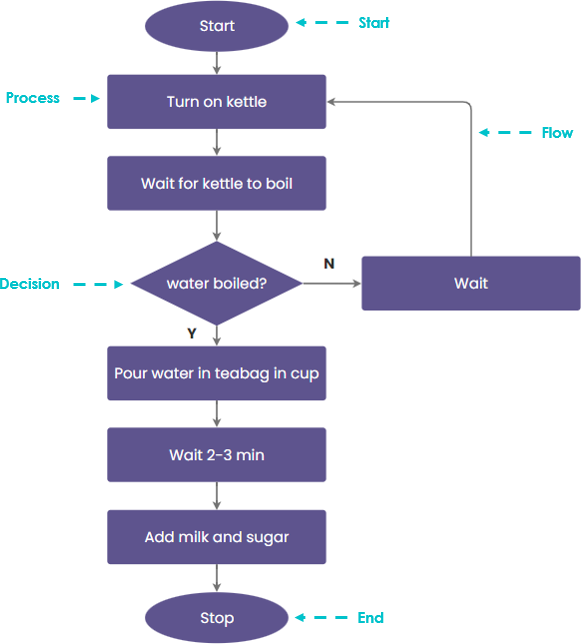
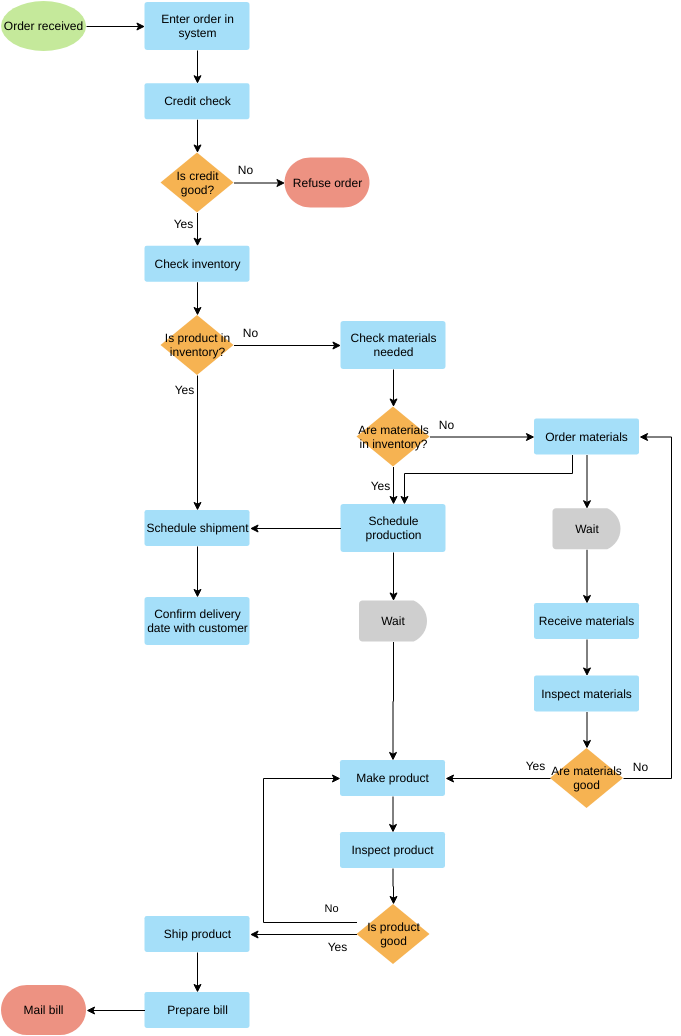
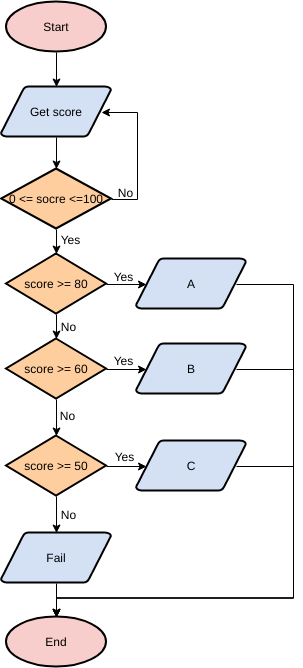
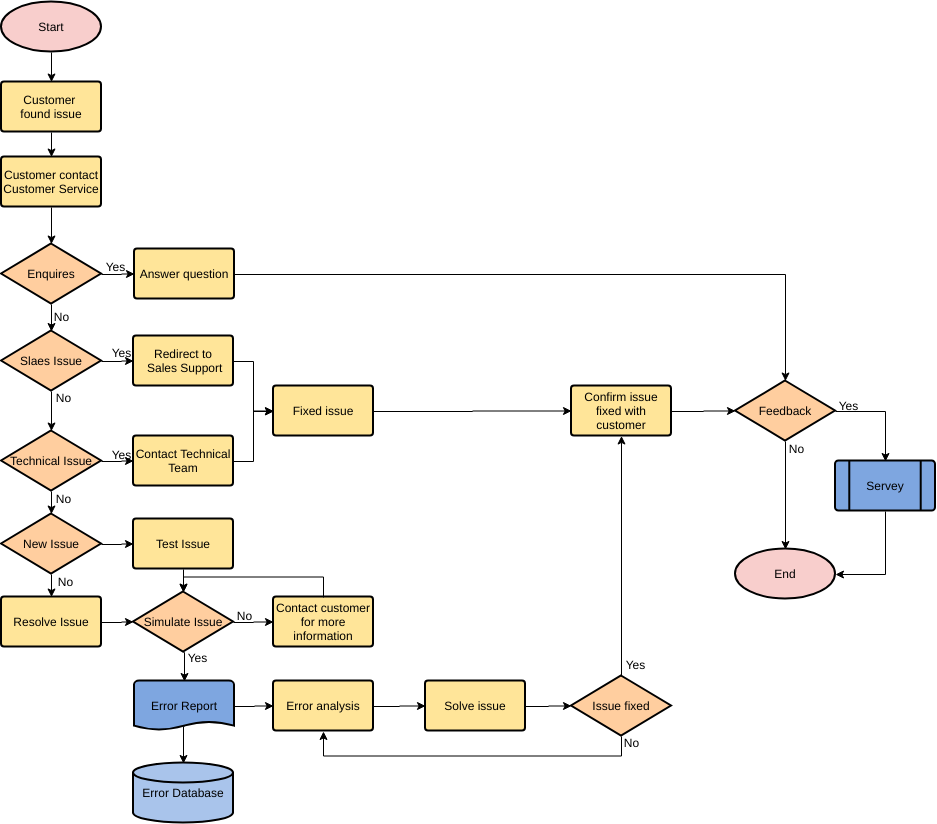
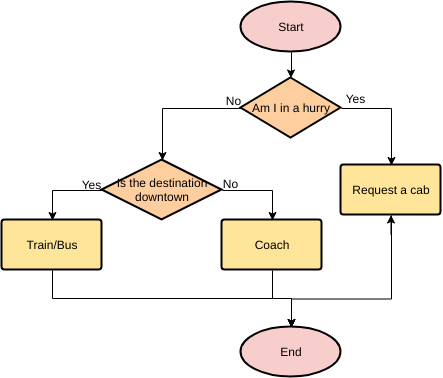
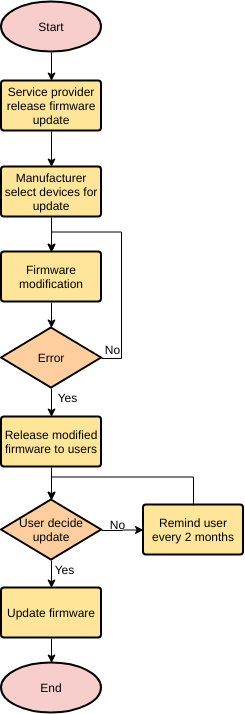
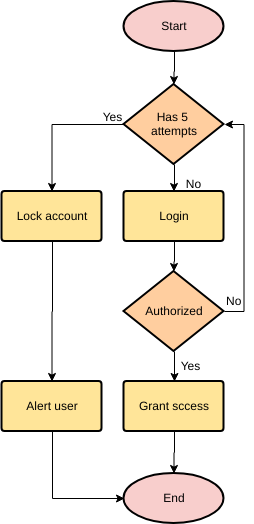
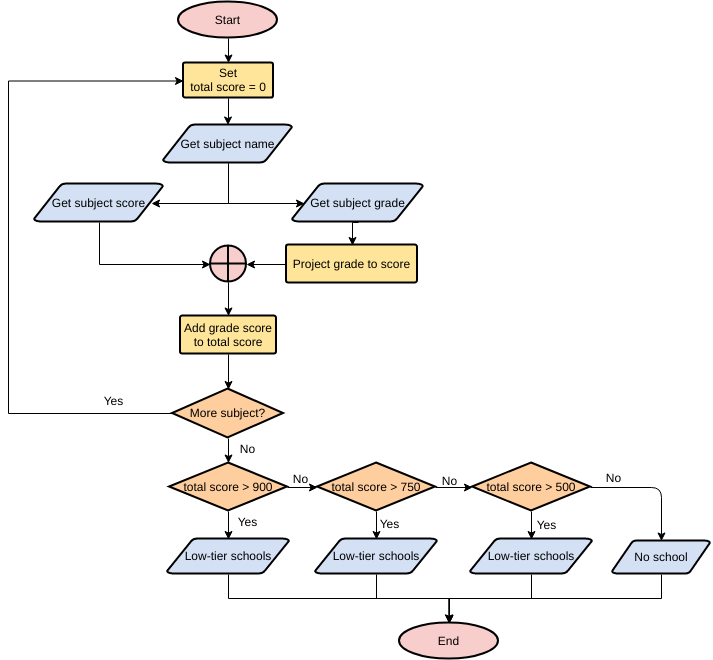
■ Пример 4.  Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.

Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.

Решение.

1. Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
2. В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет».
3. Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».
4. Вычисляется результат выполнения алгоритма: X := 0, Y := 1.

Ответ: X := 0, Y := 1.

Алгоритмические языки

Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.

В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.

Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.

Псевдокод

Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.

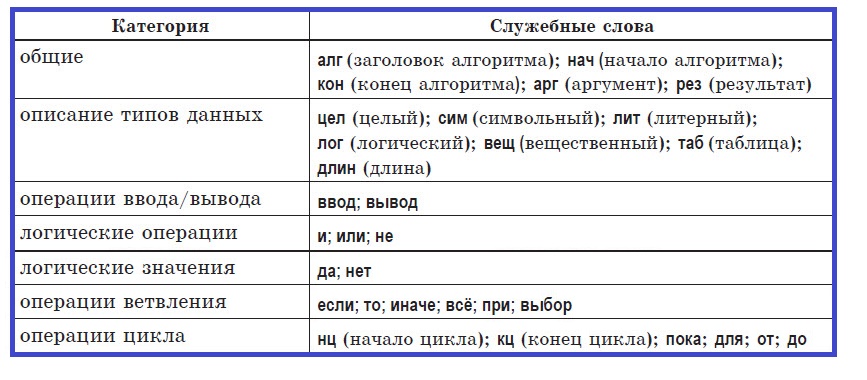
Служебные слова учебного алгоритмического языка:

Стандартная структура алгоритма

Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.

Общий вид записи алгоритма на учебном алгоритмическом языке:

В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.

В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.

Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.

Примеры заголовков алгоритмов:

В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.

Пример алгоритма вычисления гипотенузы прямоугольного треугольника:

На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.

Описание величин и действия над ними

При описании алгоритма необходимо указать названия (обозначения) всех величин, которые будут в нем найдены или использованы.

При представлении алгоритма решения в виде блок–схемы выбранные обозначения величин приводятся отдельно от блок–схемы (как объяснение к ней). Если алгоритм представлен на языке программирования, то характеристика обрабатываемых величин включается в программу. Учебный алгоритмический язык также предусматривает описание величин, используемых в алгоритме.

Все величины в алгоритме разделяют на постоянные (константы) и переменные. Константа не может изменять свои значения в процессе работы алгоритма. Переменная может приобретать различные значения, которые сохраняются до тех пор, пока она не получит новое значение. Переменным величинам назначают имена. Таким образом, переменная — это именуемая величина, которая в процессе выполнения алгоритма может приобретать и хранить различные значения.

В алгоритмическом языке не существует специальных правил именования переменных. Однако их названия не должны совпадать со служебными словами алгоритмического языка. Во многих языках программирования для имен можно использовать только латинские буквы, цифры, знак подчеркивания. Имена обязательно должны начинаться с буквы, при этом строчные и прописные буквы в именах не различаются. В одном алгоритме не могут существовать разные объекты с одинаковыми именами. Все имена являются уникальными. Имена переменных и констант стараются выбирать так, чтобы они напоминали их смысл. Например, имена переменных и констант: S, p12, result, итог.

При представлении алгоритма на алгоритмическом языке именуются не только величины, но и сам алгоритм, и другие объекты. Имя алгоритма выбирают так же, как и имена переменных.

Величина — переменная, с которой связывается определенное множество значений. Этой величине присваивается имя (в языках программирования его называют идентификатор).

Значение — то, чему равна переменная в конкретный момент. Значение переменной можно задать двумя способами: присваиванием и с помощью процедуры ввода.

Тип переменной определяет диапазон всех значений, которые может принимать данная переменная, и допустимые для нее операции. Существует несколько предопределенных типов переменных. К стандартным типам относятся числовые, литерные и логические типы.

Числовой тип предназначен для обработки числовых данных. Различают целый и вещественный числовые типы. Целый тип в учебном алгоритмическом языке обозначается служебным словом цел, к нему относятся целые числа некоторого определенного диапазона. Они не могут иметь дробной части, даже нулевой. Число 123,0 является не целым, а вещественным числом. Вещественные величины относятся к вещественному типу данных и обозначаются в учебном алгоритмическом языке служебным словом вещ. Такие величины могут отображаться двумя способами: в форме с фиксированной запятой (например, 0,0511 или –712,3456) и с плавающей запятой (те же примеры: 5,11*10^-2 и –7,123456*10²).

Над числовыми данными можно выполнять арифметические операции и операции сравнения.

Над целыми числами можно также выполнять две операции целочисленного деления div и mod. Операция div обозначает деление с точностью до целых чисел (остаток от деления игнорируется). Операция mod позволяет узнать остаток при делении с точностью до целых чисел. Например, результатом операции 100 div 9 будет число 11, а результатом 100 mod 9 — число 1.

Литерный тип представляет собой символы и строки, он дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов. Эти последовательности заключаются в двойные кавычки: «результат», «sum_price». В качестве символов могут быть использованы буквы, цифры, знаки препинания, пробел и некоторые другие специальные знаки (возможными символами могут быть символы таблицы ASCII). В учебном алгоритмическом языке литерные величины обозначаются лит.

Над литерными величинами возможны операции сравнения и слияния. Сравнение литерных величин производится в соответствии с их упорядочением: «a» < «b», «b» < «с» и т. д. Слияние (конкатенация) литерных величин приводит к образованию новой величины: «пол» + «е» образует «поле».

Логический тип определяет логические переменные, которые могут принимать только два значения — истина (True) или ложь (False). Над логическими величинами можно выполнять все стандартные логические операции.

Команды учебного алгоритмического языка

Учебный алгоритмический язык использует следующие команды для реализации алгоритма:

ОПЕРАЦИЯ ПРИСВАИВАНИЯ

Ко всем типам величин может быть применена операция присваивания, которая обозначается знаком «:=» и служит для вычисления выражения, стоящего справа, и присваивания его значения переменной, указанной слева. Например, если переменная H имела значение 12, а переменная М — значение 3, то после выполнения оператора присваивания H := М + 10 значение переменной H изменится и станет равным 13.

Вычисления в операторе присваивания выполняются справа налево: сначала необходимо вычислить значение выражения справа от знака присваивания. Поэтому допустимы конструкции вида H := Н + 10. В этом случае сначала будет вычислено выражение в правой части (12 + 10), а его результат будет присвоен в качестве нового значения переменной Н (значение 22).

Для оператора присваивания обязательно должны быть определены значения всех переменных в его правой части. Кроме того, типы данных в левой и правой части должны соответствовать друг другу.

ВВОД И ВЫВОД ДАННЫХ

В процессе работы алгоритма происходит обработка исходных данных для получения выходных (результирующих) данных. В процессе этого преобразования могут быть найдены некоторые промежуточные результаты. Входные данные должны быть переданы алгоритму («введены»), а по окончании работы алгоритм должен вывести результат.

При записи алгоритма с помощью блок–схемы ввод и вывод данных отображаются с помощью блоков ввода/вывода (параллелограммов). При этом только указывается перечень данных для ввода или вывода, а сам процесс не детализируется.

Описание алгоритма средствами псевдокода может вовсе не предусматривать команды ввода или вывода данных. В заголовке алгоритма указывается, какие данные являются аргументами, какие — результатами работы алгоритма. Считается, что аргументы будут предоставлены до выполнения алгоритма, результаты будут выведены после его выполнения, и описывается лишь процесс превращения аргументов в результаты.

В записи алгоритма с помощью учебного алгоритмического языка для операций ввода/вывода используются команды ввод и вывод. После этих служебных слов указывается список ввода или вывода. Элементы этих списков перечисляются через запятую.

Список ввода может содержать только имена переменных. После выполнения команды ввод алгоритм получит значения перечисленных в списке переменных.

Список вывода может содержать имена переменных, константы и выражения. Если в списке вывода указано имя переменной, будет выведено ее значение. Если список вывода содержит выражение, будет выведен результат его вычисления. Текстовые константы следует записывать в списке вывода в кавычках (выводиться они будут без кавычек).

Если при выполнении алгоритма ввести значения 20 и 10, то переменная v примет значение 20, а переменная t — значение 10. По окончании работы алгоритма будет выведен результат:

Путь 200 м

Тот же результат был бы получен, если бы изменить строку вывода на

вывод «Путь «, v * t, » м»

Конспект по информатике «Алгоритм. Свойства алгоритмов. Блок-схемы. Алгоритмические языки».

Вернуться к Списку конспектов по информатике.

Схема — это абстракция какого-либо процесса или системы, наглядно отображающая наиболее значимые части. Схемы широко применяются с древних времен до настоящего времени — чертежи древних пирамид, карты земель, принципиальные электрические схемы. Очевидно, древние мореплаватели хотели обмениваться картами и поэтому выработали единую систему обозначений и правил их выполнения. Аналогичные соглашения выработаны для изображения схем-алгоритмов и закреплены ГОСТ и международными стандартами.

На территории Российской Федерации действует единая система программной документации (ЕСПД), частью которой является Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем» [1]. Не смотря на то, что описанные в стандарте обозначения могут использоваться для изображения схем ресурсов системы, схем взаимодействия программ и т.п., в настоящей статье описана лишь разработка схем алгоритмов программ.

Рассматриваемый ГОСТ практически полностью соответствует международному стандарту ISO 5807:1985.

Содержание:

1. Элементы блок-схем алгоритмов
2. Примеры блок-схем
3. Нужны ли блок-схемы? Альтернативы

Элементы блок-схем алгоритмов

Блок-схема представляет собой совокупность символов, соответствующих этапам работы алгоритма и соединяющих их линий. Пунктирная линия используется для соединения символа с комментарием. Сплошная линия отражает зависимости по управлению между символами и может снабжаться стрелкой. Стрелку можно не указывать при направлении дуги слева направо и сверху вниз. Согласно п. 4.2.4, линии должны подходить к символу слева, либо сверху, а исходить снизу, либо справа.

Есть и другие типы линий, используемые, например, для изображения блок-схем параллельных алгоритмов, но в текущей статье они, как и ряд специфических символов, не рассматриваются. Рассмотрены лишь основные символы, которых всегда достаточно студентам.

	Терминатором начинается и заканчивается любая функция. Тип возвращаемого значения и аргументов функции обычно указывается в комментариях к блоку терминатора.
	В ГОСТ определено множество символов ввода/вывода, например вывод на магнитные ленты, дисплеи и т.п. Если источник данных не принципиален, обычно используется символ параллелограмма. Подробности ввода/вывода могут быть указаны в комментариях.
	В блоке операций обычно размещают одно или несколько (ГОСТ не запрещает) операций присваивания, не требующих вызова внешних функций.
	Блок в виде ромба имеет один вход и несколько подписанных выходов. В случае, если блок имеет 2 выхода (соответствует оператору ветвления), на них подписывается результат сравнения — «да/нет». Если из блока выходит большее число линий (оператор выбора), внутри него записывается имя переменной, а на выходящих дугах — значения этой переменной.
	Вызов внешних процедур и функций помещается в прямоугольник с дополнительными вертикальными линиями.
	Символы начала и конца цикла содержат имя и условие. Условие может отсутствовать в одном из символов пары. Расположение условия, определяет тип оператора, соответствующего символам на языке высокого уровня — оператор с предусловием (while) или постусловием (do … while).
	Символ «подготовка данных» в произвольной форме (в ГОСТ нет ни пояснений, ни примеров), задает входные значения. Используется обычно для задания циклов со счетчиком.
	В случае, если блок-схема не умещается на лист, используется символ соединителя, отражающий переход потока управления между листами. Символ может использоваться и на одном листе, если по каким-либо причинам тянуть линию не удобно.
	Комментарий может быть соединен как с одним блоком, так и группой. Группа блоков выделяется на схеме пунктирной линией.

Примеры блок-схем

В качестве примеров, построены блок-схемы очень простых алгоритмов сортировки, при этом акцент сделан на различные реализации циклов, т.к. у студенты делают наибольшее число ошибок именно в этой части.

Сортировка вставками

Массив в алгоритме сортировки вставками разделяется на отсортированную и еще не обработанную части. Изначально отсортированная часть состоит из одного элемента, и постепенно увеличивается.

На каждом шаге алгоритма выбирается первый элемент необработанной части массива и вставляется в отсортированную так, чтобы в ней сохранялся требуемый порядок следования элементов. Вставка может выполняться как в конец массива, так и в середину. При вставке в середину необходимо сдвинуть все элементы, расположенные «правее» позиции вставки на один элемент вправо. В алгоритме используется два цикла — в первом выбираются элементы необработанной части, а во втором осуществляется вставка.

В приведенной блок-схеме для организации цикла используется символ ветвления. В главном цикле (i < n) перебираются элементы необработанной части массива. Если все элементы обработаны — алгоритм завершает работу, в противном случае выполняется поиск позиции для вставки i-того элемента. Искомая позиция будет сохранена в переменной j в результате выполнения внутреннего цикла, осуществляющем сдвиг элементов до тех пор, пока не будет найден элемент, значение которого меньше i-того.

На блок-схеме показано каким образом может использоваться символ перехода — его можно использовать не только для соединения частей схем, размещенных на разных листах, но и для сокращения количества линий. В ряде случаев это позволяет избежать пересечения линий и упрощает восприятие алгоритма.

Сортировка пузырьком

Сортировка пузырьком, как и сортировка вставками, использует два цикла. Во вложенном цикле выполняется попарное сравнение элементов и, в случае нарушения порядка их следования, перестановка. В результате выполнения одной итерации внутреннего цикла, максимальный элемент гарантированно будет смещен в конец массива. Внешний цикл выполняется до тех пор, пока весь массив не будет отсортирован.

На блок-схеме показано использование символов начала и конца цикла. Условие внешнего цикла (А) проверяется в конце (с постусловием), он работает до тех пор, пока переменная hasSwapped имеет значение true. Внутренний цикл использует предусловие для перебора пар сравниваемых элементов. В случае, если элементы расположены в неправильном порядке, выполняется их перестановка посредством вызова внешней процедуры (swap). Для того, чтобы было понятно назначение внешней процедуры и порядок следования ее аргументов, необходимо писать комментарии. В случае, если функция возвращает значение, комментарий может быть написан к символу терминатору конца.

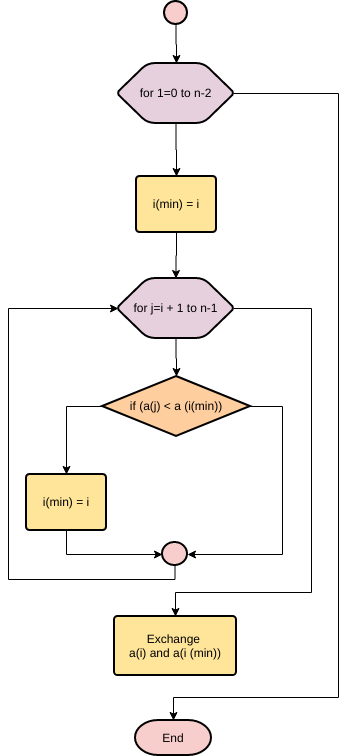
Сортировка выбором

В сортировке выбором массив разделяется на отсортированную и необработанную части. Изначально отсортированная часть пустая, но постепенно она увеличивается. Алгоритм производит поиск минимального элемента необработанной части и меняет его местами с первым элементом той же части, после чего считается, что первый элемент обработан (отсортированная часть увеличивается).

На блок-схеме приведен пример использования блока «подготовка», а также показано, что в ряде случаев можно описывать алгоритм более «укрупнённо» (не вдаваясь в детали). К сортировке выбором не имеют отношения детали реализации поиска индекса минимального элемента массива, поэтому они могут быть описаны символом вызова внешней процедуры. Если блок-схема алгоритма внешней процедуры отсутствует, не помешает написать к символу вызова комментарий, исключением могут быть функции с говорящими названиями типа swap, sort, … .

На блоге можно найти другие примеры блок-схем:

• блок-схема проверки правильности расстановки скобок арифметического выражения [2];
• блок-схемы алгоритмов быстрой сортировки и сортировки слиянием [3].

Часть студентов традиционно пытается рисовать блок-схемы в Microsoft Word, но это оказывается сложно и не удобно. Например, в MS Word нет стандартного блока для терминатора начала и конца алгоритма (прямоугольник со скругленными краями, а не овал). Наиболее удобными, на мой взгляд, являются утилиты MS Visio и yEd [5], обе они позволяют гораздо больше, чем строить блок-схемы (например рисовать диаграммы UML), но первая является платной и работает только под Windows, вторая бесплатная и кроссплатфомренная. Все блок-схемы в этой статье выполнены с использованием yEd.

Частные конторы никакие блок-схемы не используют, в книжках по алгоритмам [6] вместо них применяют словесное описание (псевдокод) как более краткую форму. Возможно блок-схемы применяют на государственных предприятиях, которые должны оформлять документацию согласно требованиям ЕСПД, но есть сомнения — даже для регистрации программы в Государственном реестре программ для ЭВМ никаких блок-схем не требуется.

Тем не менее, рисовать блок-схемы заставляют школьников (примеры из учебников ГОСТ не соответствуют) — выносят вопросы на государственные экзамены (ГИА и ЕГЭ), студентов — перед защитой диплом сдается на нормоконтроль, где проверяется соответствие схем стандартам.

Разработка блок-схем выполняется на этапах проектирования и документирования, согласно каскадной модели разработки ПО, которая сейчас почти не применяется, т.к. сопровождается большими рисками, связанными с ошибками на этапах проектирования.

Появляются подозрения, что система образования прогнила и отстала лет на 20, однако аналогичная проблема наблюдается и за рубежом. Международный стандарт ISO 5807:1985 мало чем отличается от ГОСТ 19.701-90, более нового стандарта за рубежом нет. Там же производится множество программ для выполнения этих самых схем — Dia, MS Visio, yEd, …, а значит списывать их не собираются. Вместо блок-схем иногда применяют диаграммы деятельности UML [6], однако удобнее они оказываются, разве что при изображении параллельных алгоритмов.

Периодически поднимается вопрос о том, что ни блок-схемы, ни UML не нужны, да и документация тоже не нужна. Об этом твердят программисты, придерживающиеся методологии экстремального программирования (XP) [7], ходя даже в их кругу нет единого мнения.

В ряде случаев, программирование невозможно без рисования блок-схем, т.к. это один процесс — существуют визуальные языки программирования, такие как ДРАКОН [8], кроме того, блок-схемы используются для верификации алгоритмов (формального доказательства их корректности) методом индуктивных утверждений Флойда [9].

В общем, единого мнения нет. Очевидно, есть области, в которых без чего-то типа блок-схем обойтись нельзя, но более гибкой альтернативы нет. Для формальной верификации необходимо рисовать подробные блок-схемы, но для проектирования и документирования такие схемы не нужны — я считаю разумным утверждение экстремальных программистов о том, что нужно рисовать лишь те схемы, которые помогают в работе и не требуют больших усилий для поддержания в актуальном состоянии [10].

Список использованных источников:

1. ГОСТ 19.701–90 (ИСО 5807–85) «Единая система программной документа­ции».
2. Алгоритм. Свойства алгоритма \ https://pro-prof.com/archives/578
3. Алгоритмы сортировки слиянием и быстрой сортировки \ https://pro-prof.com/archives/813
4. yEd Graph Editor \ https://www.yworks.com/products/yed
5. Книги: алгоритмы \ https://pro-prof.com/books-algorithms
6. Рамбо Дж., Якобсон А., Буч Г. UML: специальный справочник. -СПб.: Питер, 2002. -656 с.
7. Кент Бек Экстремальное программирование: разработка через тестирование – СПб.: Питер – 2003
8. Визуальный язык ДРАКОН \ https://drakon.su/
9. Шилов Н.В. Верификация шаблонов алгоритмов для метода отката и метода ветвей и границ. Моделирование и анализ информационных систем, ISSN 1818 – 1015, т.18, №4, 2011
10. Брукс Ф., Мифический человеко — месяц или как создаются программные системы. СПб. Символ Плюс, 1999 — 304 с. ил.

Что это такое? Блок-схема алгоритма отображает в графическом виде последовательность операций и переходные фазы. Каждому действию соответствует определенная фигура (ромб, квадрат, овал и т. д.), поэтому располагать их нужно в правильном порядке.

Как составить? В любой блок-схеме существуют обязательные элементы: начало, конец, линии связи. Также необходима нумерация для понимания направления чтения. Остальные действия зависят от того, какой именно алгоритм нужно описать.

Суть алгоритмов

Алгоритмом называют конечную последовательность конкретных действий, выполняя которые, исполнитель достигает определенной цели.

Итогом прохождения всех шагов должен быть изначально заданный результат (например, некие выходные данные). Для выполнения этого процесса по мере необходимости могут создаваться и использоваться промежуточные данные. Они выходными являться не будут и нужны исключительно для обеспечения всей работы.

Любой алгоритм нужно наделять определенными свойствами. Наиболее важную роль играют:

• Дискретность. Общая задача разделяется на отдельные, последовательно выполняемые шаги. Это, как правило, простейшие действия, порядок которых строго определен. Каждый шаг представляет собой инструкцию или команду, выполнение которой должно начинаться только тогда, когда выполнена предыдущая команда в этой последовательности.
• Конечность. Количество шагов должно быть конечным. Иными словами, результат необходимо получить по завершении строго определенного числа команд в алгоритме.
• Понятность. Все шаги необходимо формулировать так, чтобы исполнитель их полностью понимал. То есть алгоритм должен состоять только из команд, входящих в систему компетенций данного человека.

• Детерминированность. Каждую команду, а также порядок выполнения всех команд необходимо предварительно четко и однозначно определить. При этом на результат выполнения каждого шага не должна влиять никакая сторонняя информация. Необходимо выстроить команды так, чтобы конечная цель алгоритма обеспечивалась только формальным выполнением четких и последовательных инструкций. Исполнителю при этом не нужно вникать в смысл команд. Благодаря такому подходу итоговый результат будет всегда одинаковым и предсказуемым независимо от того, кто выполняет эту работу.
• Массовость. Один алгоритм призван решать сразу комплекс однотипных задач, определяемый заданным диапазоном входной информации.

Алгоритмы могут быть представлены в нескольких формах:

• Текстовая запись. Команды записываются обычным текстом на каком-либо языке. Порядок выполнения определяется нумерацией. Действия описываются произвольно и максимально конкретно.

  

  

  Читайте также

• Блок–схема. Команды отображаются графически, в виде блок-схемы из геометрических фигур.
• Алгоритмические языки. Алгоритм строится с использованием специального искусственного языка, состоящего из определенной системы обозначений.
• Псевдокод. Обычный язык комбинируется с алгоритмическим. Последний берется за основу для описания базовых структур алгоритма.

Что такое блок-схема алгоритма

Как упоминалось выше, алгоритм может быть схематически представлен в виде блок-схемы. Этот вид графики также широко используется для представления любых процессов и систем в самых разных отраслях деятельности человека. С помощью блок-схемы выполняется документирование, изучение, планирование, совершенствование и объяснение сложных процессов путем превращения их в простые и логичные диаграммы.

Для описания конкретных действий используются геометрические фигуры: прямоугольники, ромбы, овалы и т. д. Последовательность шагов и направление процессов отображается соединительными стрелками.

Существует несколько видов блок-схем алгоритма, которые отличаются в числе прочего сложностью исполнения, начиная от простейших и нарисованных от руки эскизов, заканчивая сложными, спроектированными на компьютере диаграммами. Блок-схемы, учитывая многообразие всех вариаций, могут быть использованы в самых разных областях жизнедеятельности и, соответственно, по-разному называться.

Так, в зависимости от отрасли, встречаются схемы процессов, функциональные блок-схемы, модели и нотации бизнес-процессов, схемы технологических процессов. Все это имеет тесную связь с другими популярными разновидностями схем (например, с некоторыми диаграммами).

Составляющие блок-схемы алгоритма

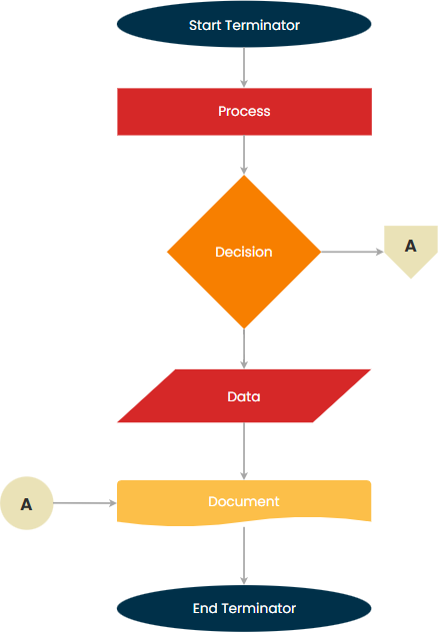
Блок-схемы создаются из различных блоков, соединяемых между собой линиями со стрелками. Таким образом отображается поток управления. Далее разберем более подробно каждый тип блоков.

Терминал

Представляет собой овальную область, которой обозначают начало и конец выполнения программы. В любом алгоритме, изображенном в виде блок-схемы, присутствует как минимум два таких овала, которые ограничивают собой данный алгоритм.

Данные

Блок рисуется в виде параллелограмма, содержащего внутри входные или выходные данные. Обычно здесь размещают информацию, поступающую в алгоритм извне, и результат, который в итоге он выдает.

Процесс

Выглядит как прямоугольник, служит для записи основного программного кода. Процесс является ключевым элементом алгоритма, отражающим суть всей блок-схемы.

Скачать
файл

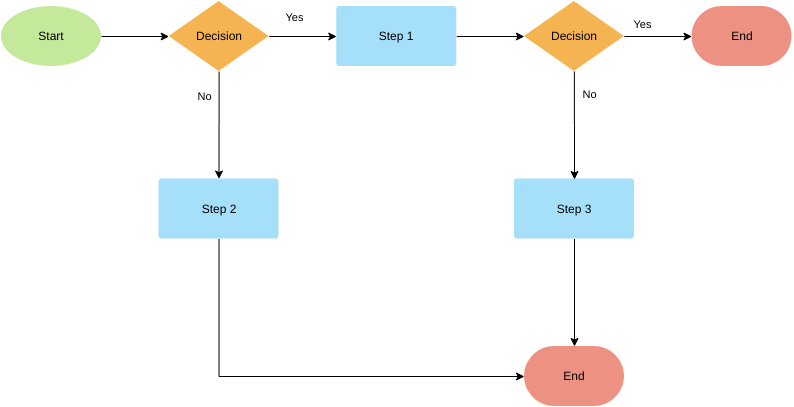
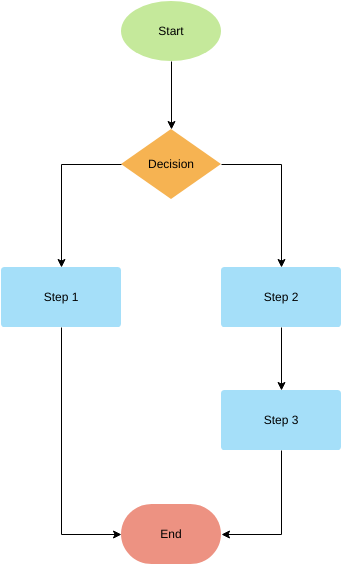
Решение

Данный блок рисуется в виде ромба и предназначен для управляющих и условных операторов какого-либо языка программирования (например, if или «больше» и «меньше»). Здесь всегда предлагается на выбор один из двух вариантов: «да» или «нет».

Поток

Обозначается в виде стрелки, представляя собой собственно поток какого либо процесса или алгоритма с указанием направления. Таким способом обеспечивается высокая читаемость программы.

Ссылка на странице

Выглядит как окружность с расположенными внутри символами. Такая ссылка дает понять, что блок-схема продолжает дальнейшие шаги алгоритма. Когда схема достаточно длинная, для экономии места внутри данной окружности в качестве ссылки размещают одну цифру. Этот же символ должен быть использован в продолжении схемы.

Правила составления блок-схемы

Чтобы составить блок-схему алгоритма грамотно, необходимо следовать приведенным ниже принципам.

• Начало и конец схемы обязательно ограничиваются соответствующими блоками в одном экземпляре.
• Начальный блок должен быть соединен с конечным линиями связи.
• Линии потока необходимо рисовать из всех блоков, кроме конечного.
• Все блоки нумеруются по порядку слева направо и сверху вниз. Номера ставятся в верхнем левом углу с разрывом начертания.
• Между всеми блоками обеспечивается взаимная связь через линии, определяющие последовательность выполнения команд. Движение потока в обратном порядке от принятого по умолчанию обязательно обозначается стрелками.
• Используемые в схеме линии могут быть входящими или выходящими. Это разделение относительное. Для одного линия, выходящая из одного блока, для другого уже будет являться входящей.
• Начальный блок имеет лишь выходящие линии потока. Соответственно, в конечный блок линии могут только входить.
• Поскольку движение потока идет сверху вниз, входящие линии принято изображать сверху от блока, а выходящие — снизу. Это в целом упрощает чтение блок-схемы.
• Линии потока могут обрываться. При этом места разрывов необходимо помечать специальными соединительными элементами.
• Чтобы блок-схема легче читалась, допускается описательную часть выносить в комментарии.

Разделение блок-схемы

Построение блок-схемы зачастую связано с определенными трудностями, среди которых:

• слишком малое место для размещения на одной странице;
• сложности в связывании всех элементов непосредственно друг с другом.

Устранить эти проблемы можно путем разбивки всей блок-схемы алгоритма программы на несколько фрагментов и последующего соединения этих фрагментов специальными соединительными элементами.

Используемые при этом соединители подписываются уникальными номерами, состоящими из двух частей. Это нужно для определения соответствия соединительных линий друг другу. Принадлежность частей уникального номера соединительному элементу обеспечивается записью данного номера на каждом фрагменте блок-схемы. Общие правила разделения приведем ниже.

• Места разрыва схемы обозначаются соединительным блоком. Каждое такое соединение маркируется уникальным номером.
• Использоваться должны только машинно-независимые элементы.
• Представление в блок-схеме каждого шага не является обязательным. Важно отобразить только ключевые этапы выполнения программы.
• Переменные и блоки желательно именовать наглядными и запоминаемыми словами.

И самое главное условие — сформированный алгоритм должен быть понятен любому программисту.

Востребованность блок-схем

В небольших компаниях для построения алгоритмов обычно применяют лаконичную словесную форму (псевдокод). Блок-схемы же вероятнее всего встречаются на государственных предприятиях, где действуют требования по оформлению документации ЕСПД. Однако даже при регистрации программного обеспечения в Госреестре можно обойтись без этих схем.

И все же современные учебные программы в школах и вузах учитывают умение рисовать данного вида графику. Вопросы, посвященные блок-схемам, встречаются на выпускных и государственных экзаменах. Студенты перед дипломной защитой также должны проверять свою работу на соответствие стандартам построения схем.

Программное обеспечение сегодня почти не разрабатывается по устаревшей каскадной модели, так как при этом часто на этапах проектирования возникают ошибки. Но когда разработка по такой модели все же ведется, применяются именно блок-схемы записи алгоритма.

Во всем мире наблюдается значительное отставание образовательной системы от технического прогресса. Отечественный устаревший стандарт ГОСТ 19.701-90 в целом схож с международным ISO 5807:1985.

Привлекает мир кодирования и создания программ? На курсе программиста с нуля до Junior вы освоите основы, познакомитесь с языками и инструментами разработки, и станете готовы к созданию своих первых проектов в IT-индустрии.

Более актуальные модификации до сих пор не разработаны. За рубежом все еще продолжают создавать специализированное программное обеспечение для проектирования блок-схем (Dia, MS Visio, yEd).

Есть немногочисленные примеры применения более совершенных диаграмм деятельности UML, хотя эти диаграммы показывают свою эффективность лишь при описании параллельных алгоритмов.

В среде разработчиков порой возникает мнение о бесполезности блок-схем и даже UML. Некоторые убеждены в том, что и документация для разработки тоже не требуется. Впрочем, об этом чаще говорят сторонники так называемого экстремального программирования.

Для определенных задач разработки использование блок-схем все же требуется. В частности, это необходимо, когда программы создаются в визуальных средах программирования (например, ДРАКОН). Также с помощью блок-схем верифицируются алгоритмы. То есть, в соответствии с методом индуктивных утверждений Флойда формально доказывается их корректность.

Пока что можно сделать вывод, что единого мнения касательно необходимости блок-схем нет. Безусловно, в некоторых областях деятельности без них пока не обойтись в отсутствие альтернативы. Формальная верификация требует создавать блок-схемы выполнения алгоритма, хотя для непосредственного проектирования и документирования это уже не нужно.

Здесь стоит прислушаться к утверждению «программистов-экстремалов» о том, что имеет смысл рисовать лишь те схемы, которые действительно полезны в работе и при этом не требуют слишком больших усилий для рисования и актуализации.

Супер простое руководство по блок-схемам

Что такое блок-схема?

Блок — схема — это графическое представление операций, выполняемых системой обработки данных.
операций в системе. Часто лучший способ понять проблему — нарисовать диаграмму. Диаграммы обычно дают нам более полную картину ситуации, чем короткий набор слов или фраз. Однако сочетание визуальных символов (фигур) и текста представляет собой очень мощный инструмент для общения и решения проблем. Алгоритмы могут разрабатываться быстрее, если для их представления создается блок-схема. Блок-схемы гораздо легче понять, чем алгоритмы.

Блок-схема показывает:

• показывает логику алгоритма
• выделяет отдельные шаги и их взаимосвязь
• например, управление потоком от одного действия к другому

Символы блок-схемы

Блок-схемы имеют много стандартных символов. В блок-схемах используются блоки различной формы для представления различных типов инструкций. Фактические инструкции написаны внутри коробок. Эти блоки соединены сплошными линиями со стрелками, указывающими направление потока блок-схемы. Направление потока блок-схемы. Блоки, используемые в блок-схемах, стандартизированы и имеют определенные значения. Символы для этих блок-схем были разработаны Американским национальным институтом стандартов (ANSI).

Элемент	Описание	Символ
СТАРТ/СТОП терминатор	START и один терминатор STOP на всей блок-схеме. Если логика программы включает паузу, она также обозначается символом терминала.
Ввод, вывод	Этот символ используется для обозначения любой функции ввода/вывода в программе. Таким образом, если есть какой-либо ввод в программу через устройство ввода, такое как клавиатура, лента, устройство чтения карт и т. д., это будет указано на блок-схеме с помощью символа ввода/вывода. Точно так же все инструкции вывода для вывода на такие устройства, как принтеры, плоттеры, магнитные ленты, диски, мониторы и т. д., обозначены символом ввода/вывода.
Решение	Представляет собой точку принятия решения в процессе, обычно требующую ответа «да» или «нет», а затем переход к различным частям блок-схемы.
Ссылка на страницу включения/выключения.	Представляет соединение с другим процессом.
Линии потока	Указывает направление потока. Горизонтальные стрелки изображают процедуры или линейную последовательность событий, а вертикальные стрелки обозначают второстепенные или высшие навыки и знания.
Обработать	Символ процесса используется для представления арифметических инструкций и инструкций по перемещению данных на блок-схеме. Все арифметические процессы сложения, вычитания, умножения и деления обозначены символом процесса. Логический процесс перемещения данных из одного места памяти в другое также представлен в блоке процесса.

Блок-схема с первого взгляда: Иллюстрация символов

Блок-схема должна иметь начальную точку и одну или несколько конечных точек и должна располагаться в направлении сверху вниз и слева направо.

Простую блок-схему, показывающую описанные выше символы, можно увидеть ниже:

ИЗМЕНИТЬ ЭТОТ ПРИМЕР БЛОК-СХЕМЫ

Представление алгоритма в структурированном программировании с помощью блок-схемы

Блок-схемы часто используются для представления алгоритмов структурного программирования. Блок-схемы описывают структуру и логику алгоритма, а также последовательность операций, которые необходимо выполнить при решении проблемы.

• Блок-схемы полезны для сложных программ, содержащих множество ветвей, поскольку они описывают взаимосвязь между отдельными ветвями и циклами.
• Они также помогают обнаруживать и исправлять ошибки в логике и разрабатывать более эффективные структуры.

Наконец, блок-схема — отличный инструмент для документирования программы. Он обеспечивает удобное средство связи между программистами и непрограммистами.

Последовательность — ряд процессов/шагов, которые следуют по порядку.

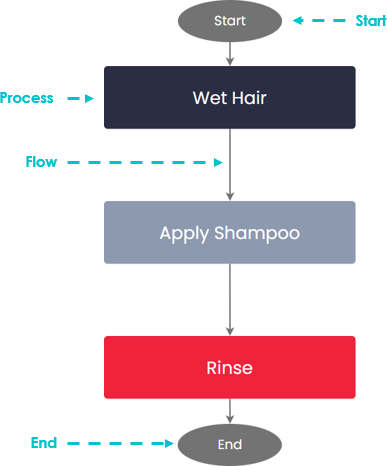
Например, помыть голову;
1. Намочите волосы
2. Нанесите шампунь
3. Смойте

ИЗМЕНИТЬ ЭТОТ ПРИМЕР БЛОК-СХЕМЫ

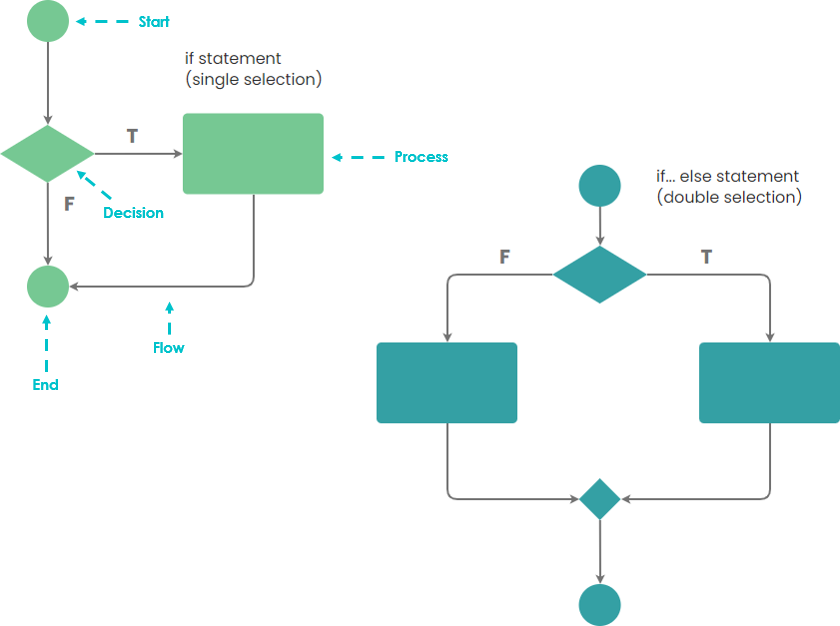
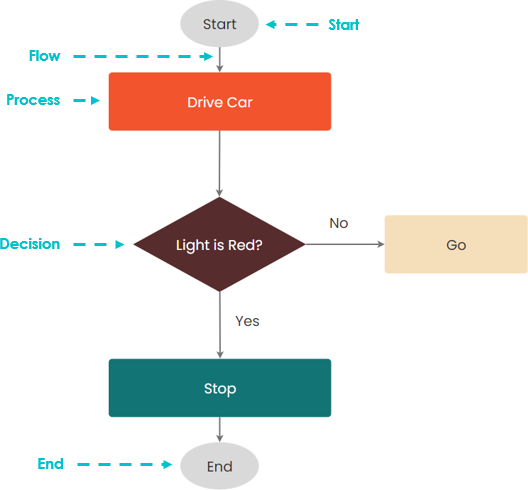
Выбор — существует условие, которое может изменить порядок или типы процессов, которым необходимо следовать.

ПРИМЕР БЛОК-СХЕМЫ: РЕДАКТИРОВАТЬ СЕЙЧАС

Например, ЕСЛИ горит красный свет, ТО Я остановлюсь, ИНАЧЕ Я поеду.

ПРИМЕР БЛОК-СХЕМЫ В ИНТЕРНЕТЕ: РЕДАКТИРОВАТЬ СЕЙЧАС

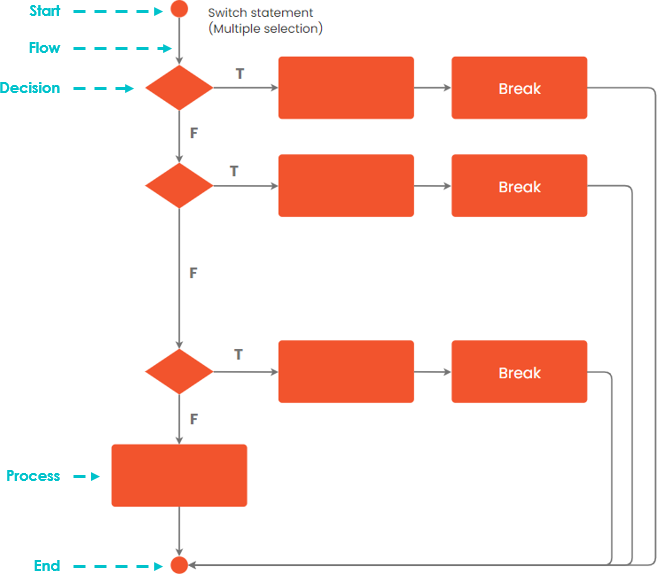
Заявление о случае

РЕДАКТИРОВАТЬ БЛОК-СХЕМУ: ОНЛАЙН-КОНСТРУКТОР БЛОК-СХЕМ

Повторение . Часто нам может потребоваться выполнить один и тот же набор процессов несколько раз, и мы можем выполнить цикл, который выполняет один и тот же набор действий снова и снова, пока не возникнет условие остановки. Невыполнение условия остановки приведет к тому, что процесс войдет в бесконечный цикл.

РЕДАКТИРУЙТЕ В НАШЕМ ОНЛАЙН-РЕДАКТОРЕ БЛОК-СХЕМ

Примером ЦИКЛА может быть отображение слова «ШКОЛА» на экране 7 раз.

РЕДАКТИРОВАТЬ В НАШЕМ ПРОГРАММНОМ ОБЕСПЕЧЕНИИ ДЛЯ СОЗДАНИЯ БЛОК-СХЕМ

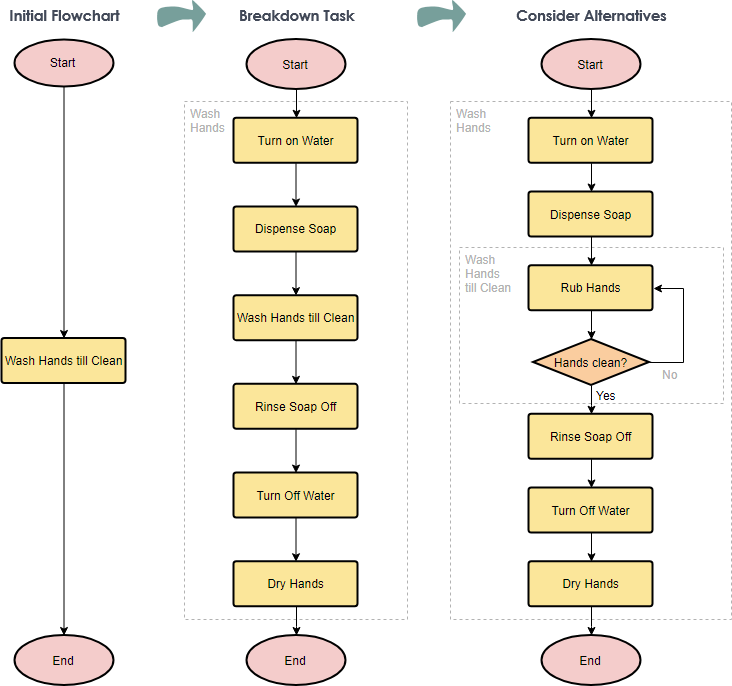
Разработайте блок-схему с пошаговым уточнением

Пошаговое уточнение — это процесс разбиения задачи программирования на ряд шагов. Вы начинаете с некоторых общих шагов для решения проблемы и уточняете каждый шаг по очереди. После уточнения каждого шага вы далее разбиваете эти общие шаги на серию более мелких подэтапов. Как только это сделано, вы продолжаете, пока не опишете проблему настолько подробно, что сможете написать код для ее решения.

Поэтапное уточнение: разработать решение проблемы путем

1. 1. изложение решения на высоком уровне
   2. уточнение шагов решения в более простые шаги
   3. повторяя шаг 2, пока шаги не станут достаточно простыми для выполнения

Поэтапное уточнение с помощью примера блок-схемы — вернуться домой

Самый эффективный способ решить сложную проблему — разбить ее на последовательно более простые подзадачи. Вы начинаете с того, что разбиваете всю задачу на более простые части. Некоторые из этих задач, возможно, сами должны быть разделены. Этот процесс называется пошаговым уточнением (или декомпозицией сверху вниз). Вы можете выполнить шаги и создать блок-схему, используя метод пошагового уточнения.

Блок-схема ниже иллюстрирует постепенное совершенствование этих четырех этапов.

• Мы совершенствуем одну вещь за раз.
• Светло-голубая трапеция показывает, как один шаг на диаграмме слева уточняется (расширяется) на следующей блок-схеме справа.

Пример пошагового уточнения блок-схемы – мытье рук

ОТРЕДАКТИРУЙТЕ ЭТОТ ПРИМЕР БЛОК-СХЕМЫ [ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ БЛОК-СХЕМЫ]

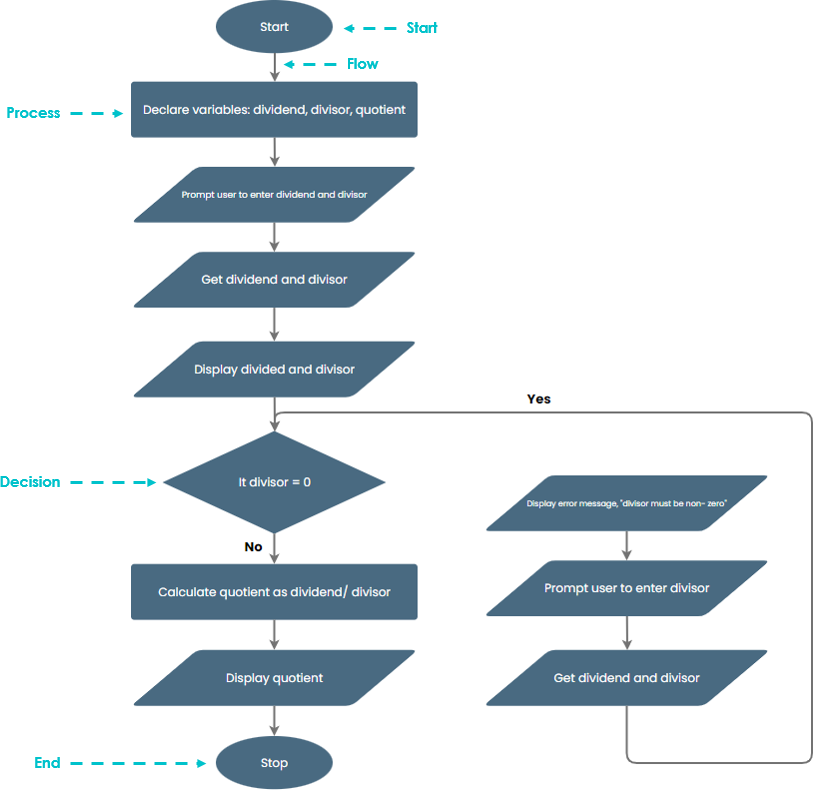
Пример блок-схемы – Решите алгоритм

Выразите алгоритм, который получает от пользователя два числа (делимое и делитель) и проверяет, не равен ли делитель нулю. Убедитесь, что делитель не равен нулю, и используйте блок-схему, чтобы показать их частное.

ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ДЛЯ СОЗДАНИЯ БЛОК-СХЕМ — ОТРЕДАКТИРУЙТЕ ЭТОТ ПРИМЕР БЛОК-СХЕМЫ [FLOWCHART MAKER]

Пример блок-схемы — процесс приготовления чашки чая теперь можно продемонстрировать более подробно:

ОНЛАЙН-РЕДАКТОР БЛОК-СХЕМ — ОТРЕДАКТИРУЙТЕ ЭТОТ ПРИМЕР БЛОК-СХЕМЫ

Пример блок-схемы: преобразование температуры по Фаренгейту в градусы Цельсия

ОТРЕДАКТИРУЙТЕ ЭТОТ ПРИМЕР БЛОК-СХЕМЫ — ОНЛАЙН-КОНСТРУКТОР БЛОК-СХЕМ

Узнайте больше о блок-схеме — на примерах

Блок-схема — это одна из наиболее широко используемых диаграмм, которая представляет алгоритм, рабочий процесс или процесс, показывая шаги в различных полях и соединяя их по порядку стрелками. Вы можете создать блок-схему с нуля или просто начать с шаблонов блок-схем, доступных в программном обеспечении для создания блок-схем Visual Paradigm Online .

Нужно вдохновение? Ниже мы собрали несколько примеров блок-схем, чтобы помочь вам начать работу. Нажмите на блок-схему, чтобы просмотреть ее, или нажмите кнопку «Редактировать», чтобы начать редактирование.

Что такое алгоритм и зачем он нужен[править]

Многое в нашей жизни подчинено правилам и инструкциям. Часть из них для нас весьма очевидна, что выполняется неосознанно. Алгоритм и все что с ним связано развивался из потребностей математики. Сейчас мы рассмотрим какие задачи математики тесно связаны с алгоритмикой. Надеюсь, что читатель или учится в школе или учился, а потому помнит вычисление корней квадратного уравнения. Для упрощения изложения мы будем рассматривать только нахождение корней, выраженных лишь действительными числами(на всякий случай напомню что это например: -1,0,1,2 и т.д.,а так же числа как: 0.5,2.5 и т.д.).

Итак мы вычисляем корни уравнения вида , где .(1)

Опишем алгоритм словесно:
Алгоритм решения квадратного уравнения

Шаг 1:взять коэффициенты a,b,c из (1 )

Шаг 2: вычислить дискриминант(D) выражения(1) по формуле:

Шаг 3:Если D>0 то:       
Если D=0 то:
Если D<0 то: действительных корней нет

Вот он алгоритм и никакой мистики. Но мы рассмотрим еще один:преобразование неправильной дроби.

Из математики нам известно,что правильная дробь эта та где числитель меньше знаменателя, а неправильная там где наоборот. Если это записать математически то получится:,где Так вот наш алгоритм должен преобразовать неправильную дробь в правильную. Опишем его как всегда словесно:(при этом под словом записать понимается записать результат на бумагу. Условимся так же что числитель обозначим буквой «a»,а буквой «b» знаменатель)
Алгоритм преобразования правильной дроби в неправильную

Шаг 1: Проверить что a>b, если нет то дробь правильная, останавливаемся иначе переход к шагу 2

Шаг 2:Разделить a на b.

Шаг 3:записать как целую часть частное от деление.

Шаг 4:Если остаток от деления неравен 0, то:
Записать как числитель новой дроби остаток от деления a на b. Записать знаменателем новой дроби знаменатель исходной дроби(b ).
иначе:завершить преобразование
шаг 5:Завершить выполнение

Вот и еще один алгоритм мы с вами увидели.Ну и наконец пример еще одного:
Довольно часто возникает задача проверки числа на четность. Четное число делится на 2 без остатка. Напишем алгоритм, который решает поставленную задачу:
Алгоритм проверки на четность

Шаг 1: взять число
Шаг 2: Проверить что число больше нуля
Шаг 3: Если число равно 0 прекратить выполнение
Шаг 4:Разделить число на 2
шаг 5: Если остаток равен 0, то числа четные, иначе нет.

Мы с вами рассмотрели 3 алгоритма теперь пора уже собственно ответить на вопрос, а что это?

Определим алгоритм как последовательность четких инструкций приводящих к выполнению поставленной задачи. Однако этого недостаточно у него есть еще 5 свойств, которые позволяют алгоритм назвать алгоритмом:

1. Конечность Это означает что алгоритм должен приводить к решению поставленной задачи за некий конечный промежуток времени Обратите внимание что все наши алгоритмы обязательно завершатся
2. Однозначность. Все инструкции в этих алгоритмах трактуются однозначно и как я надеюсь разночтений возникать не должно. Если же вам что то неизвестно из употребленных понятий, то можно найти их общепринятые определение
3. Вход Любой алгоритм должен иметь входные данные, то есть те данные к которым он будет применен.
4. Выход Любой алгоритм должен выдавать какие то данные как результат
5. Универсальность Алгоритм должен работать для любых данных, которые соответствуют типу алгоритма. Например: наш алгоритм решения квадратного уравнения должен решать свою задачу при любых параметрах, относящихся к множеству действительных чисел. Говоря проще: если разработчик заявил что это численный алгоритм работает со всеми натуральными числами, то он должен работать с любыми числами от до ,хоть с 0, хоть с 1000000 . В то же время глупо ждать от численного алгоритма корректной работы с символами
6. Эффективность Люди разрабатывают алгоритмы для решения конкретных задач и конечно же хотят найти наиболее оптимальные методы ее решения.Поэтому алгоритм можно оценить с точки зрения его эффективности а как мы еще поговорим в этой главе.

Итак мы уяснили для себя что такое алгоритм. Теперь рассмотрим пару примеров вобщем то внешне похожих на алгоритмы.

«Алгоритм» изучения науки об алгоритмах:

1. Найти хорошую книгу по алгоритмам
2. Внимательно ее читать и делать все упражнения
3. Не лениться

Читателю предоставляется возможность ответить на вопрос почему это вовсе не алгоритм самостоятельно
И еще один:

«Алгоритм» медитации:

1. Найти тихое уединенное место
2. Удобно расположиться
3. Закрыть глаза
4. Избавиться от мыслей
5. Находится в таком состоянии сколько сможете и захотите

Аналогично предлагается читателю показать, что это псевдоалгоритм.

Представление алгоритмов для ЭВМ[править]

Перво наперво нам стоит с вами запомнить, что наш железный друг весьма глуп. Да это действительно так: он выполняет только то, что ему скажут при чем в самом буквальном смысле слова. В упражнениях к этой главе мы рассмотрим один пример такой наивности компьютера. Далее поскольку интерпретация естественного языка, т.е. того на которым мы говорим весьма сложная задача, которая требует возможности обобщения, учета внешних условий, возможности самостоятельной переработки информации наконец, то компьютер не может выступать никоим образом в роли понимающего естественный язык.Поэтому были придуманы специальные формы записи алгоритмов для компьютера, которые отличаются следующими свойствами:

• Однозначностью каждого своего элемента
• Строгой стандартизованностью

Такие формы записи называют языками программирования. Их великое множество: C,Pascal,C++,Perl,Python,ASP,PHP,Prolog,Рефал,Lisp,assembler и такой экзотичный Forth
Но на самом деле языков крайне много, несколько тысяч. Так как языки программирования, несмотря на их жесткую формализованность, все же являются выражением предпочтений их автора, его взгляда на предметную область, то всегда будут появляться новые.
Мы же рассмотрим более частный вопрос, но для нас более важный: как мы будем представлять алгоритмы.
У нас есть выбор: использовать какой либо существующий язык программирования, пвседокод или придумывать свой. Третий путь отбросим сразу автор этого курса отбросил, т.к. явно не Дональд Кнут:) Псевдокод меня то же неслишком устраивает, все ж хочется чтобы можно было «пощупать» результаты наших размышлений. Итак остается для нас путь под номером 1. Какой же язык мы выберем? У нас их будет аж три: python,C,Pascal. Но не пугайтесь вам дастотачно будет знать и одного: для быстрой иллюстрации моих утверждений в наиболее приближенной к обычным записям форме будет применяться python. Тем более он не требует никаких вещей типа компиляции линкования и т.д. Он сразу начнет все выполнять, так как интерпретируемый.Ну а окончательная реализация будет представлена на двух языках программирования для удобства всех читателей: на С и Pascal. Что ж этот вопрос мы с вами уяснили и переходим к следующему пункту: основные алгоритмические структуры.

Быстрый старт в Python[править]

Основные алгоритмические структуры[править]

Вполне возможно что читатель уже с ними хорошо знаком и все же позволю себе их вам напомнить.

• Условный оператор—Его назначение позволить программисту закодировать процесс выбора выполнения тех или иных фрагментов алгоритма в зависимости от предыдущих вычислений.

Python:

if a>b:
 print "A great then b "
else:
 print "A less then b "

Pascal:

if a>b then
 writeln("A greate then B")
else
writeln( "A less then B")

C:

if (a>b)
 printf( "A great then b ");
else
 printf ("A less then b ");

Как видим идея этого оператора в том, чтобы выбрать на основе проверки некоего условия путь работы программы/алгоритма. Такого рода проверка называется логическим вычислением. Оно подчиняется законам булевой алгебры, которые мы рассмотрим чуть позже. Результатом такого вычисления может быть
либо: истина(true) либо ложь(false)
Этот оператор использует результат логических вычислений, если условие соблюдено, то выбирается та ветка которая идет сразу после if (то есть будет выведено «A great then b «), а если нет, то «A less then b «. Кстати не верьте мне на слово, а запустите Python и введите следующий скрипт(так называются программы на любом интерпритируемом языке):
Python:

a=7
b=6
if a>b:
 print "A great then b "
else:
 print "A less then b "

Вводите этот скрипт несколько раз изменяя значения переменных и следите за результатами.

• Оператор множественного выбора

Этот оператор позволяет реализовать нам выбор развития хода программы не из двух вариантов, а из многих.

a=11
if a==10:
 print "A= ",a
elif a==11:
  print "A(second branch) =  ",a
elif a==12:
 print "A(thrid branch)= ",a

Выполните этот скрипт с различными значениями переменной a и посмотрите результат.

В С оператор множественного выбора выглядит так:

int a;
switch(a)
  {
   case 10:
      {
       printf("A(first branch) =%d",a);
       break;
      }
   case 12:
      {
       printf("A(second branch) =%d",b);
       break;
      } 
    default:
       {
          printf("A(default branch) = %d",c);
        }

  }

• Циклы:

Цикл— это конструкция языка/алгоритма, которая позволяет выполнить заданные действия многократно

1. Циклы с условием:

Python:

a=1
while a<=11:
 print a 
 a=a+1

Pascal:

a:=1;
while a<=11 do 
begin
writeln( a);
a:=a+1;
end;

C:

a=1;
while (a<=11){ 
writeln( a);
a=a+1;
}

Логика выполнения этой конструкции такова:
Сначала проверяется на истинность условие после слова while(в нашем случае что переменная a должна быть или меньше, или равна 11) Если условие истинно, то
переходим к выполнение цикла, то есть то что после слова while. Печатаем значение переменной a. После выполнения тела цикла, то есть того что мы печатали после cлова while, программа снова проверит условие в случае истинности снова будет выполнен цикл, а если оно ложно то нет и будет выполнена следующая инструкция после тела цикла.
Теперь давайте подумаем зачем написано a=a+1? Возможно вы уже догадались, а может и нет, если нет, то: цикл проверяет условие на истинность. От того что мы печатаем значение переменной само ее значение никак не изменится, а значит условие всегда будет истинным и цикл не остановится никогда. Вы вынуждены будете отключить саму программу для прекращения цикла.То есть вот схема выполнения:

1. Проверить условие цикла
2. Если истинно:

Выполнить тело цикла
изменить значение переменной, используемой для проверки условия

1. вернутся к шагу 1

Иначе:

  Выйти из цикла

1. Цикл со счетчиком:

Очень часто перед нами возникает задача выполнения цикла известное число раз и для удобства записи был придуман цикл for.
Алгоритм его выполнения:

1. присвоить начальное значение переменной, по которой производится проверка условия(счетчику)
2. Выполнить действия в теле цикла
3. Уменьшить или увеличить значение счетчика. Все зависит от условий применения цикла

Язык python немного иначе трактует цикл for. В нем for служит для прохода программы по элементам структур данных типа массив, список и т.д.
Python:

a=[] #сформируем список
for i in a:#переменной i последовательно присваиваются все элементы списка 
 print  a

Pascal:

for a:=1 to 12 do
begin
writeln('Iteration#',a);
writeln("go to the next iteration");
end;

С:

for (int i=0;i<=12;i++)
{
printf('Iteration#%d',a);
printf("go to the next iteration");
}

Слово итерация в данном случае обозначает выполнение тела цикла.Важный момент: любой цикл for может быть заменен while циклом, но не наоборот. Если у вас есть сомнения какой из циклов применять, то запомните простое правило: если неизвестно заранее сколько раз будет выполнен цикл, то применяйте while цикл, а если заранее известно сколько раз выполнится цикл то for.На этом закончим обзор основных алгоритмических структур.

Примеры записи алгоритмов[править]

Давайте запишем те самые алгоритмы в словесной форме, в форму понятную для ЭВМ.
Итак:

• Программа вычисления корней квадратного уравнения:

# -*- coding: utf-8 -*-
from  math import * #сообщаем python где найти функцию извлечения корня   
a=input("Введите коэффициент а")#запрос к пользователю о вводе значения коэфф. a
b=input("Введите коэффициент b")#запрос к пользователю о вводе значения коэфф. b
c=input("Введите коэффициент c")#запрос к пользователю о вводе значения коэфф. c
d=b**2-4*a*c #вычислим дискрминант 
if d>0: #если дискриминант больше нуля...
    x=(-b+sqrt(d))/2*a
    x1=(-b-sqrt(d))/2*a
    print "Первый корень=",x,"Второй=",x1
elif d==0: #равен 0
    x=-b/2*a
    print "x:",x
elif d<0:#меньше 0
 print "Это уравнение не имеет действительных корней"

• Алгоритм преобразования неправильной дроби:

# -*- coding: utf-8 -*-

a=input("Введите числитель")
b=input("Введите знаменатель")
if a<b:
    print "Вы ввели правильную дробь"
    print a,'/',b
elif a%b==0: print a/b
elif a>b: print a/b ,a%b,'/',b

• Алгоритм проверки на четность

# -*- coding: utf-8 -*-

a=input("Введите число")
if a%2==0:
    print "Вы ввели четное число"
else:
      print "Вы ввели нечетное число"

Как видите хоть записано иначе чем словами, но запись отражает все те действия которые мы довольно долго описывали словесно. Вас могла удивить строчка

1. -*- coding: utf-8 -*- Но к алгоритмам она не имеет никакого отношения, она нужна затем чтобы Python нормально воспринял кириллические буквы, что обеспечивает кодировка UTF-8

Некоторые важные теоретические вопросы[править]

Здесь будут обсуждены некоторые основополагающие понятия теории алгоритмов. Здесь будет дано лишь общее представление о них, а более подробную информацию о них вы найдете в литературе к этому параграфу и в статьях Википедии.

Тезис Чёрча-Тьюринга[править]

С одной стороны наука об алгоритмах очень точная наука и опирается на довольно точный математический аппарат, но с другой само понятие алгоритма не слишком математично. Вот как раз и поговорим о том как же его пытались определить.Одним из определений алгоритма является т.н. Тезис Чёчра-Тьюринга.
Тезис Чёрча-Тьюринга:Любой алгоритм в интуитивном понятии может быть выполнен машиной Тьюринга. И здесь у вас может возникнуть вопрос: что такое машина Тьюринга?Ее описание мы дадим в отдельном пункте, а пока определимся так: это абстрактная ЭВМ с основными элементами характерными для обычного компьютера. Так вот машина Тьюринга как понятие позволила делать обобщенный анализ алгоритмов. При таком анализе мы можем сосредоточится на самих алгоритмах и оперировать их чистыми свойствами, а не тем как ведет себя некий алгоритм на данной машине,с ее аппаратными особенностями. Более того фактически тезис Чёчра-Тьюринга кроме того ввел следующий постулат: любой алгоритм который может быть выполнен на физическом устройстве можно выполнить и на машине Тьюринга, а от себя мы продолжим утверждение: а значит он может быть проанализирован. Этот же тезис позволил поставить проблему алгоритмической неразрешимости многих вопрос не только информатики, но даже алгебры и других математических дисциплин.Кстати основная проблема алгоритмической неразрешимости заключается в том, что для некоторого класса задач не может быть найдено алгоритма, обладающего свойством универсальности или как его еще называют: массовости.Одним из примеров такой проблемы является проблема останова алгоритма. Она формулируется так: требуется найти универсальный алгоритм, который бы отвечал на вопрос: остановится ли заданный алгоритм выполняемый на произвольной машине Тьюринга.
Было доказано что это алгоритмически не разрешимая задача. Предлагаю вам, уважаемый читатель, самостоятельно доказать алгоритмическую не разрешимость этой проблемы. Если же у вас не получилось или вам интересно, то приведу свое доказательство:
Итак допустим мы имеем некий алгоритм. С нас спрашивают найти некий метод доказательства конечности или бесконечности выполнения произвольного алгоритма.

Фактически нас просят разработать еще один алгоритм. Однако перед нами сразу возникнет дилемма: как доказать конечность выполнения самого проверяющего алгоритма? Ведь это алгоритм и он сам должен обладать свойствами: конечности, универсальности и т.д. Ни то ни другое мы не можем получить, т.к. фактически мы пытаемся один алгоритм всего лишь противопоставить другому, но при этом не имеем возможности ответить на вопрос о конечности выполнения обоих.А значит он как минимум не удовлетворяет одному из свойств обязательных для алгоритма.
Какой важный вывод мы должны сделать из всего описанного? Не все задачи имеют алгоритмическое решение!

Теперь рассмотрим для полноты картины различные модели вычислений

Модели вычислений[править]

Здесь мы рассмотрим различные виды абстрактных вычислительных машин, которые сыграли важную роль в развитии теории алгоритмов. Здесь требуются некоторые пояснения: сама теория алгоритмов родилась среди математиков и хотя люди ее развивавшие понимали что вычислительная техника это очень перспективно и будет прикладной областью теории, но самой вычислительной техники, которая была бы способна выполнять произвольные алгоритмы не было. Например Черч и Тьюринг писали работы по проблемам вычислимости еще в 30-ые годы, а первые модели компьютеров, которые могли бы выполнять алгоритмы появились лишь в 40-ые и 50-ые годы. Однако их появление не решает проблемы. Даже сейчас когда стандартизация аппаратных частей компьютеров позволяет пользоваться аппаратурой разных производителей и т.д. мы можем столкнутся с тем что, например, на одном компьютере процессор мощнеее ем у другого и т.д. Тогда встает вопрос: а что мы измерим при анализе быстродействия алгоритма:скорость машины на примере алгоритма или все же скорость алгоритма. Но даже если каким-то волшебным образом мы учтем вклад аппаратной части машины и отделим его от алгоритмического, то увидим иную проблему: это НАША конфигурация машины, а программы выполняются на совершенно разных системах: от тостеров и до суперкомпьютеров, считающих модели Большого взрыва. Это что ж нам так тестировать на всех возможных моделях аппаратуры?

Математики нашли выход из этой затруднительной ситуации в те же 30-ые годы ХХ века. Они предложили некоторую логическую модель устройства, которое может читать\писать данные в и из памяти, а так же обрпащаться к различным участкам памяти. Такие модели и стали абстрактными исполнителями алгоритмов. Ниже некоторые из них будут освещены детальней

Машина Тьюринга[править]

Машина Тьюринга это очень важное понятие в нашем предмете.Опишем составные части этой машины и правила ее функционирования.Перед этим хочу сделать важное замечание: машина Тьюринга не является попыткой отразить все нововведения, которые в огромном количестве внедряются в различные компоненты реальных ЭВМ. Как раз наоборот эта модель разрабатывалась за тем, чтобы оставить алгоритмиста один на один с алгоритмом. Другой ее важной целью было предложить простой набор команд, который бы позволил проводить четкие исследования по сложности каждого шага алгоритма и делать общие выводы о алгоритме. Поэтому не удивляйтесь такой «древности» машины Тьюринга.

Вот ее описание из соотв. статьи Википедии:

В состав машины Тьюринга входит бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.

Из вышеизложенного тезиса Черча-Тьюринга следует, что машина Тьюринга способна имитировать другое исполнительное устройство, если заданы правила перехода из одного состояния в другое.Машина Тьюринга была первым абстрактным исполнительным устройством, которая позволила обосновать возможность оценки сложности алгоритмов.
Описание реальной машины Тьюринга производится как показано ниже:

Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: q_ia_j→q_i1a_j1d_k (если головка находится в состоянии q_i, а в обозреваемой ячейке записана буква a_j, то головка переходит в состояние q_i1, в ячейку вместо a_j записывается a_j1, головка делает движение d_k, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации <q_i, a_j> имеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.

Пример машины Тьюринга:

Приведём пример МТ для умножения чисел в унарной системе счисления.
Машина работает по следующему набору правил:

Набор правил	Набор правил
q0*→q0R	q4a→q4aR
q01→q0R	q4=→q4=R
q0×→q1×R	q41→q41R
q11→q2aR	q4*→q51R
q21→q21L	q5*→q2*L
q2a→q2aL	q6a→q61R
q2=→q2=L	q6×→q7×R
q2×→q3×L	q7a→q7aR
q31 → q4aR	q71→q2aR
q3a→q3aL	q7=→q8=L
q3*→q6*R	q8a→q81L
q4×→q4×R	q8×→q9H

Умножим с помощью МТ 3 на 2 в единичной системе:

Протокол|center

В протоколе указаны начальное и конечное состояния МТ, начальная конфигурация на ленте и расположение головки машины (подчёркнутый символ).

При помощи данной модели Тьюринг смог формализовать понятие алгоритма, заложить основы теории вычислимости, которая является одним из важнейших разделов современной математики.
Более подробно о машине Тьюринга можно прочесть в этом викиучебнике

Машина Поста[править]

Машина Тьюринга не являлся единственной моделью вычислительного устройства, которая применялась и применяется в теории алгоритмов.Упрощенную модель абстрактной вычислительной машины предложил математик и логик Эмиль Пост. Опять же процитируем Викистатью:

МП состоит из каретки (или считывающей и записывающей головки) и разбитой на секции бесконечной в обе стороны ленты (см. пример ниже). Каждая секция ленты может быть либо пустой — 0, либо помеченной меткой 1. За один шаг каретка может сдвинуться на одну позицию влево или вправо, считать, поставить или уничтожить символ в том месте, где она стоит. Работа МП определяется программой, состоящей из конечного числа строк. Всего команд шесть:

N.   →   J	сдвиг вправо
N.   ←   J	сдвиг влево
N.   1   J	запись метки
N.   0   J	удаление метки
N.   ? J1, J0	если в ячейке нет метки, то перейти к j1 строке программы, иначе перейти к j2 строке программы.
N.   Stop	остановка

где N. — номер строки, J — строка на которую переходит управление далее.

Для работы машины нужно задать программу и ее начальное состояние (т. е. состояние ленты и позицию каретки). После запуска возможны варианты:

• работа может закончиться невыполнимой командой (стирание несуществующей метки или запись в помеченное поле);
• работа может закончиться командой Stop;
• работа никогда не закончится.

Как видим перед нами ЭВМ с ограниченным набором команд. Машина Поста опять же явилась одним из важных шагов в развитии теории алгоритмов, самых ее фундаментальных вопросов. Ну что ж теперь переходим гораздо ближе к прикладным вопросам: оценке временной сложности алгоритмов.

Сложность алгоритмов и методы ее оценки[править]